快速排序算法介绍

前言

提到排序，我们最熟悉的应该是选择排序法和冒泡法了吧？这两种排序方法的时间复杂度现在可以知道，是O(n^2)。对于这两种方法，我们在进行排序时发现大部分元素被重复进行了很多次相同的判断，看上去很没有必要对吧？那么现在就介绍一种新的排序方法，看标题顾名思义，一种加快速度的排序方法。

思路

首先，我们来想一件事情。对于一堆数字，现在要求将这些数字进行排序，假如我们随便以一个数为一个标准，称之为“基数”，把大于基数的数重新放在一堆，小于基数的数放在另一堆，那么在进行排序判断的时候，在某一堆的数字是不是就不用和另一堆的数字进行比较了对吧？进行判断时只需要同一堆的数字之间进行比较就可以了，最终排序结果就是：小堆(小于基数)、基数、大堆(大于基数)。我们现在将一堆数字只做了一次分堆，减少了一定程度的时间复杂度，那么，如果我们继续把分出来的堆进行再分堆，那么时间复杂度又会有所减少，将这个过程一直重复下去，时间复杂度就会越来越小，而这个过程看上去有递归的味道了，所以也是可以实现的。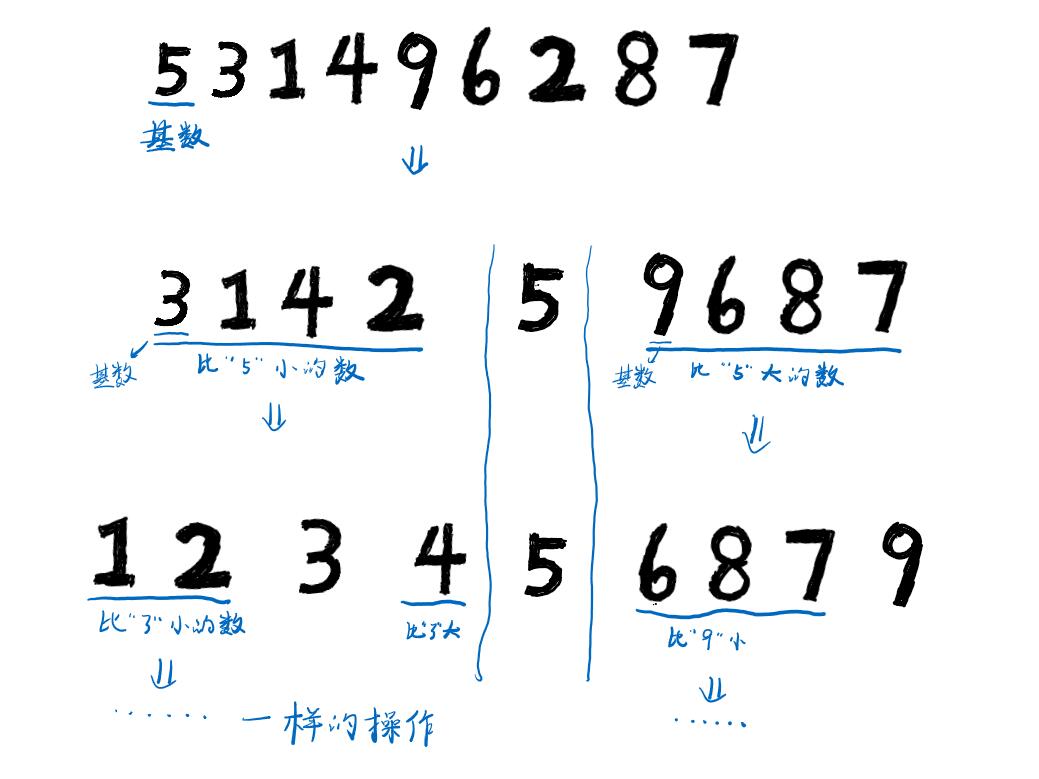

代码

#include<cstdio>
#include<iostream>
using namespace std;
int main(){
    void qsort(int* a,int curl,int curr);
    int a[10];
    for(int i=0;i<10;i++) cin>>a[i];
    qsort(a,0,9);
    for(int i=0;i<10;i++) cout<<a[i]<<"  ";
    return 0;
}
void qsort(int* a,int curl,int curr){
    if(curl>=curr) return;
    int l=curl,r=curr,temp;
    int base=a[curl];
    while(l<r){
        while(a[r]>=base&&r>l)
            r--;
        while(a[l]<=base&&l<r)
            l++;
        if(l<r){
            temp=a[l];
            a[l]=a[r];
            a[r]=temp;
        }
    }
    a[curl]=a[r];
    a[r]=base;
    qsort(a,curl,r-1);
    qsort(a,r+1,curr);
}