狄克斯特拉算法介绍

对于寻找某副图里的最短路径条数我们可以用光度深搜的算法，因为我们尽可能希望在近的地方找到答案，现在我们看另一个问题。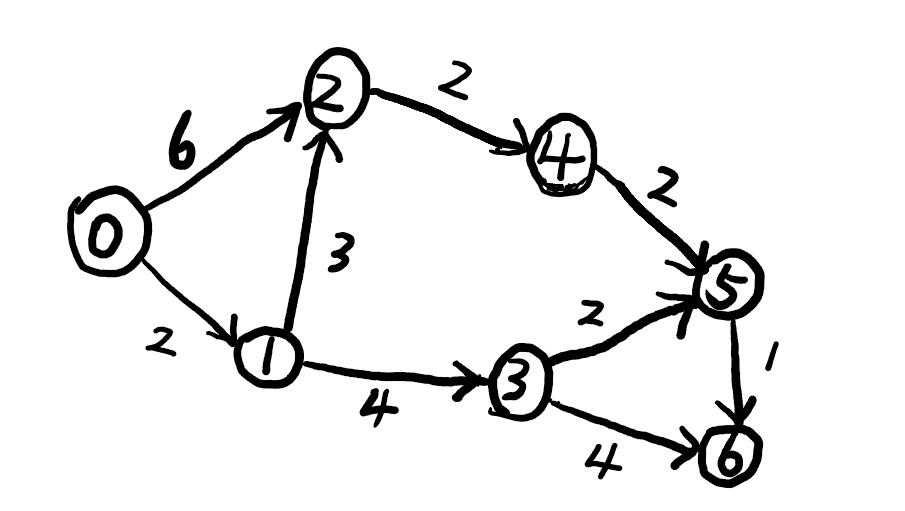

如图，同样也是与路径有关的问题，但是该图中边上的数字表示从某地点到另一地点所需要花费的时间，那么现在问一下：从 0 到 6 所花的最少时间是多少？具体路径怎么走？

思路

显然，我们现在不能从路径的条数入手了，因为我们要求的是最少时间，而图中最短的路径似乎不是我们想要的答案。还记得回溯法吗？就是先尝试着从起点走到终点，然后检查是否满足要求即可，同样我们可以借鉴这种思想。
我们先尝试着把从起点到终点的每一条路都走一遍，并且每走一次计算出所花的时间，把所有的路走完后取最小值就可以了。但取最小值，不是说每一次走完把时间存在数组里，然后再去找最小值，这样就降低了运行效率<s>而且略显low...
尽然我们想得到最小值，那么我们保证每走到一个地点所花的时间是最小值就可以了，也就是说走到每一个点所花的时间都是最少的，那么一直走下去走到终点的时候得到的时间自然也就是最少的了，这个就和那个 矩阵取数 的原理差不多。

不多说了，直接上代码吧，代码有点繁冗，重点看思路和注释吧。

代码

#include<cstdio>
#include<iostream>
using namespace std;
int vis[10],time[10][10];
struct Point{                        //每一个节点的属性
    int neibor[10];            //每一个节点的邻居
    int parent;           //节点的父节点，用来确定最终路径，这个对结果没有影响，可以不要
}point[7];            //图中有 7 个节点
int main(){
    void find_fastest_route(int p);
    void route(int r);
    int n;
    cout<<"输入邻居，以 -1 结束"<<endl;
    while(1){                         //连接邻节点，且有方向，方向为箭头方向
        cin>>n;
        if(n==-1) break;               //结束标志   -1
        for(int i=0;(getchar())!='n';i++){            //遇到回车说明该节点的邻居已经输入完了
            cin>>point[n].neibor[i];
        }
    }
    int a,b,mint;
    cout<<"输入两点间所花时间，以 0 0 0 结束"<<endl;
    while(1){                                         //输入两点间所花的时间
        cin>>a>>b>>mint;
        if(!a&&!b&&!mint) break;               //结束标志  0 0 0
        time[a][b]=mint;
    }
    find_fastest_route(0);                    //调用遍历路径的函数
    cout<<endl<<vis[6]<<endl;
    route(6);                           //输出具体路径，这个对结果的数值没有影响。
    return 0;
}
void find_fastest_route(int p){
    if(p==6) return;                         //已经到终点，终止继续走下去
    for(int i=0;point[p].neibor[i];i++){            //有邻居
        int cost=vis[p]+time[p][point[p].neibor[i]];    //经过该节点到该节点的邻居所用的时间
        if(cost<vis[point[p].neibor[i]]||!vis[point[p].neibor[i]]){   //讨论没有走过时，时间默认为0
            vis[point[p].neibor[i]]=cost;          //如果走该条路径所花时间更少，则更新时间
            point[point[p].neibor[i]].parent=p;             //更新父节点
        }
        find_fastest_route(point[p].neibor[i]);           //继续向终点走下去
    }
}
void route(int r){            //输出具体路径，这个就是递归原理，就不说了
    if(r==0){
        cout<<r;
        return;
    }
    route(point[r].parent);
    cout<<"-->"<<r;

结果

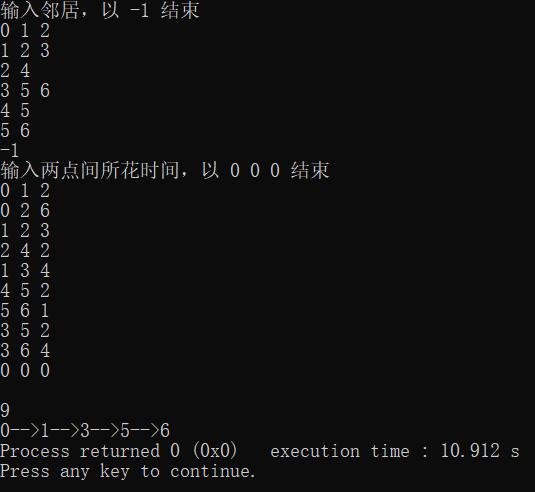
输入邻居时：第一个数字表示某个节点，后面的数字表示该节点的邻居
输入所花时间时：前两个数字表示两个节点，且方向为从前到后，第三个数字为所花时间
其中对输入的格式有一定的要求，比如连接邻居的时候，因为是以回车作为结束标志的，所以每输入一组数据的最后不能有空格和其他字符；还有需要按箭头的方向顺序来输入数据，否则在遍历（继续走下去）的时候会发生方向反向，来回徘徊甚至陷入死循环等情况。