广度优先搜索算法介绍

介绍

广度优先搜索 又称为 宽度优先搜索 ，也就是在进行搜索的过程中，先对最近的位置进行搜索，再到第二近的位置进行搜索......简单来说，就是先搜索完浅层，再去搜索深层的策略。举个例子：

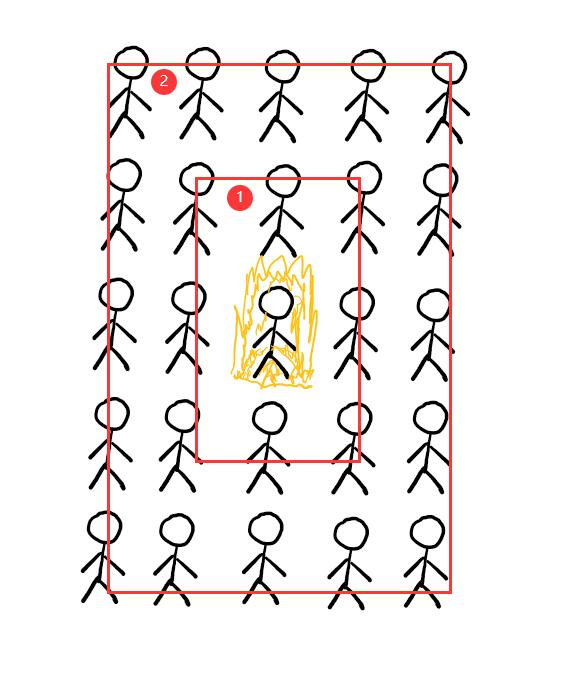
假如你是最中心的那个人，没错，就是战斗力看起来爆表的那位！满载一身功力的你再也忍受不了孤独，想会一会其他人来展示一下自己高超的武功，可你在与其他人PK之前需要确认一下对方的战斗力，只和符合战斗力要求的人PK，同时又希望找的人离自己越近越好，你与在场的所有人的关系值都是0，也就是说不会特意的优先去找哪个人（同时排除他们来找你的可能性，不要问为什么），因此你会先从离你最近的一圈人中去找，找到了符合条件就直接进行PK，如果没有找到，再去下一圈的人里去找.......以此类推，直到找到人为止。如果每个人都找了，却发现没有一个能符合条件，emmm.....高手总是寂寞的！

示例

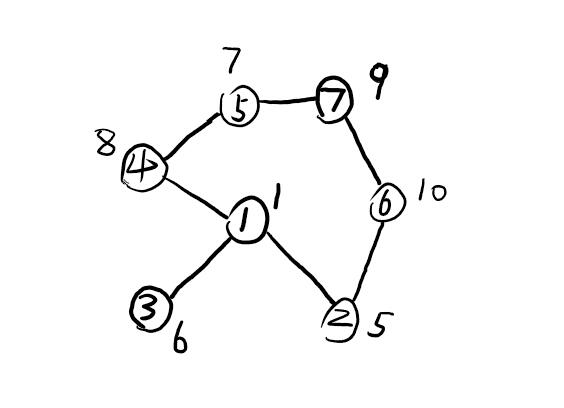
现在给出一个图，圈内表示节点序号，节点序号旁边的数字表示该节点的数值，来确认图中是否存在某一个数，它在哪个节点？

思路

从1号节点出发，利用广搜的原理，先检查3，4，5号节点的数值，如果有要找的数字，则返回节点序号，如果没有则继续查找第二层的节点，即5，6号节点....一直找下去，直到所有节点找完即可。

那么具体的实现是怎样的呢？我们可以发现，在进行广搜时，是先把第一层的节点列入了搜索对象，并在所有的第一层节点搜索完后再列入第二层节点进行搜索，由此大家可以联想到一个线性表，那就是“队列”。队列的出入规则是先入先出，正好可以符合广搜的要求，在C++里专门有队列的功能，它在 queue 的头文件里，关于queue的具体使用方法可以百度，只要知道队列的原理和具体指令，简单地使用一下还是比较容易的。

代码

#include<cstdio>
#include<iostream>
#include<queue>
using namespace std;
int jd[8]={0,1,5,6,8,7,10,9};           //图中信息
int graph[8][5]={{},{2,3,4},{1,6},{},{1,5},{4,7},{2,7},{5,6}};     //图中信息：节点的“邻居”
int vis[8];
int main(){
    int N,result;
    cin>>N;
    queue<int>jd_check;
    jd_check.push(1);
    while(!jd_check.empty()){
        int check=jd_check.front();
        jd_check.pop();
        if(jd[check]==N){
            result=check;
            break;
        }
        vis[check]=1;
        for(int i=0;graph[check][i];i++){
            if(!vis[graph[check][i]]) jd_check.push(graph[check][i]);
        }
    }
    cout<<"The number can be fount at "<<result;
    return 0;
}

也许你会问了，竟然已经写了jd这个数组了，直接一个for循环判断数组中是否存在这个值不就可以了吗？

嗯，的确是这样的，但在这里只想说明一点，就是广搜具有查找某样东西的功能，但真正利用广搜的时候不会只解决这一个问题，我们继续往下看。

again

图中有7座小岛，每一座岛上有一个数字卡片，其中圈内表示岛的序号，圈旁边的表示卡片的数字。现在你正处在1号岛上，现在你的任务是找到给出的一个数字的卡片，假设每一条边的长度一样，如果这张数字存在，问最少走多少几条路可以拿到这张数字卡片？

思路

显然，这个就不是数组的问题了，这个时候依旧按照搜查的路径走，只不过在上面的基础上记录下当前所走的路的条数罢了。（当然，纯粹的用数组解决这个问题也行得通，但现在主要的是要体现一个思想方法！）

代码

#include<cstdio>
#include<iostream>
#include<queue>
using namespace std;
int jd[8]={0,1,5,6,8,7,10,9};
int graph[8][5]={{},{2,3,4},{1,6},{},{1,5},{4,7},{2,7},{5,6}};
int vis[8],edge[8];          //加了一个edge数组来记录走到某位置时所走过的路的条数
int main(){
    int N,result;
    cin>>N;
    queue<int>jd_check;
    jd_check.push(1);
    while(!jd_check.empty()){
        int check=jd_check.front();
        jd_check.pop();
        if(jd[check]==N){
            result=check;
            break;
        }
        vis[check]=1;
        for(int i=0;graph[check][i];i++){
            if(!vis[graph[check][i]]){
                jd_check.push(graph[check][i]);
                edge[graph[check][i]]=edge[check]+1;      //增加的
            }
        }
    }
    cout<<"The number can be fount at "<<result<<" and the closest route is "<<edge[result];              //多输出了一个最短路径
}

另外，这个问题还可以变，比如每一条路的长度不一样，然后问最近的距离是多少。同样的，将记录路的条数的数组改成记录所走路径的长度的数组就可以了，这里就不多说了。

这个是一个基础的算法，本人会的也不多，所以这种文字大概也只能给小白看了吧，大佬不喜勿喷！