回溯法 —— 八皇后问题

前言

回溯法是暴力求解问题的一个重要方法，先说一说回溯法的概念吧。

递归函数在递归过程发生的返回上一层重新递归调用的现象称为“回溯”。

也就是说，当递归函数递归到某一个地方时，发现没有办法继续递归下去时，就会选择返回到上一层而去另找一条递归的路径，就好比走迷宫一样，当我们走到死胡时，就会选择往回走去找探索一条路，这样的过程就是回溯。

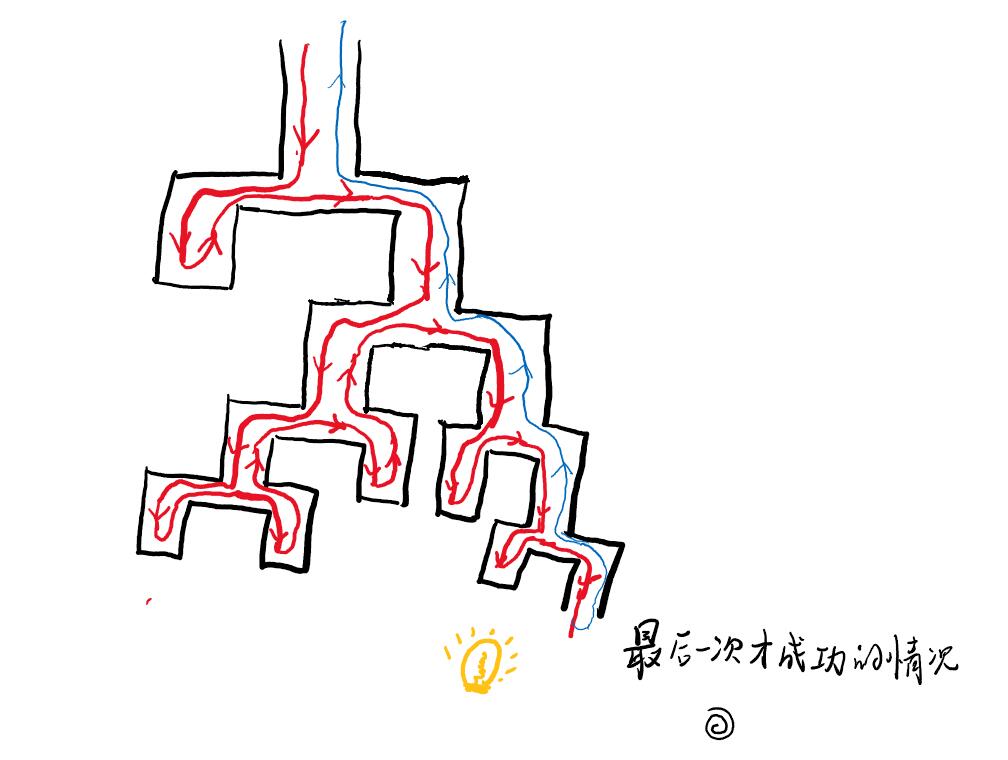
思路

首先呢，先确定好递归的过程，这个问题比较好想，就是一行一行的处理，比如先处理第一行，然后尝试把第一行的棋子放在第1列、第2列、第3列......判断放在某列时是否满足条件，如果满足条件，则进行下一行的处理，同样的对于下一行的棋子也是从第1列开始尝试，这样一来，这个过程是相同的，可以用递归来实现。

事实上吧，回溯就是递归，只不过会有条件阻挡它递归，也就是不让它乱递归，如果满足条件，就让你递归；如果不满足，那就找其他路走，所以这个回溯的话没有必要当作一个特殊的方法，就当作递归来写就行。

接下来就确定一下递归条件。根据八皇后的规则，棋子不能在同一行、同一列以及同一个对角线上（以棋子为中心的主副对角线，就是画一个规规整整的 × ），因为我们是按照一行一行来放棋子的，所以就不用考虑行冲突的问题，毕竟我们一行只放一个，那么就只需要判断某颗棋子的列上是否有其他棋子，其对角线上是否也有其他棋子就可以了，也就是将之前已经放好的棋子与现在尝试放的棋子作比较，看有没有发生冲突，以第x行和第y行的棋子两者作比较的条件为例：

x的列数 == y的列数？
x的行数+列数 == y的行数+列数？
x的行数-列数 == y的行数-列数？

其中2、3条，对于同一条主对角线上的元素，其行数-列数是一个相等的数值，对于同一副对角线上的元素，其行数+列数是一个相等的数值，所以通过判断其数值是否相等，来判断是否位于某一条对角线上。如果放在某列的棋子与之前的棋子作了比较后都没有发生冲突，说明放在该列上是满足条件的。

代码

#include<cstdio>
#include<iostream>
using namespace std;
int N,loc[21];
int main(){
    void search_loc(int row);
    cin>>N;
    search_loc(0);
    return 0;
}
void search_loc(int row){
    if(row==N){         //每一行已经成功的安排上皇后棋，输出结果
        for(int i=0;i<N;i++){
            for(int j=0;j<N;j++)
                if(loc[i]==j) cout<<"X";
                else cout<<"O";
            cout<<endl;
        }
        cout<<endl;
        return;
    }
    for(int i=0;i<N;i++){     //尝试将 row 行的棋子放在 i 列上
        int ok=1;          //判断棋子放在某处时是否合理，默认合理为1.
        loc[row]=i;
        for(int j=0;j<row;j++)
            if(loc[row]==loc[j]||loc[row]-row==loc[j]-j||loc[row]+row==loc[j]+j){  //冲突条件
                ok=0;             //放在当前列上与前面的棋子有冲突，结束判断
                break;
            }
        if(ok) search_loc(row+1);         //没有冲突，进行放置下一行的棋子。
    }
}

对于上述的代码，时间复杂度为O(n^2)，其中判断过程就是与之前放好的棋子进行比较判断是否冲突，如果没有冲突，就确认放在该列上，进行下一行棋子的放置。

通过判断的条件，我们可以发现，对于不同对角线上的元素的 (行数+列数) 或 (行数-列数)的数值一定是不同的，所以我们不妨用一个标记符号来标记已经有棋子的列和对角线，这样的话，放置某个棋子时，只需要确认该位置是否被标记过即可（这个位置是在某列或某对角线上的）

优化

#include<cstdio>
#include<iostream>
using namespace std;
int N,loc[21],vis[3][71];            //标记数组，确认某列或某对角线是否被标记
int main(){
    void search_loc(int row);
    cin>>N;
    search_loc(0);
    return 0;
}
void search_loc(int row){
    if(row==N){
        for(int i=0;i<N;i++){
            for(int j=0;j<N;j++)
                if(loc[i]==j) cout<<"X";
                else cout<<"O";
            cout<<endl;
        }
        cout<<endl;
        return;
    }
    for(int i=0;i<N;i++){
        loc[row]=i;
        if(!vis[0][i]&&!vis[1][row+i]&&!vis[2][row-i+N]){     //判断该位置是否位于被标记的某列或某条对角线上
            vis[0][i]=vis[1][row+i]=vis[2][row-i+N]=1;         //1表示标记
            search_loc(row+1);                         //进行下一行的放置
            vis[0][i]=vis[1][row+i]=vis[2][row-i+N]=0;  //进行尝试下一列时，要把当前的标记去掉（因为棋子要换位置了，要把标记撤去）
        }
    }
}

回溯法 —— 八皇后问题

前言

思路

代码

优化

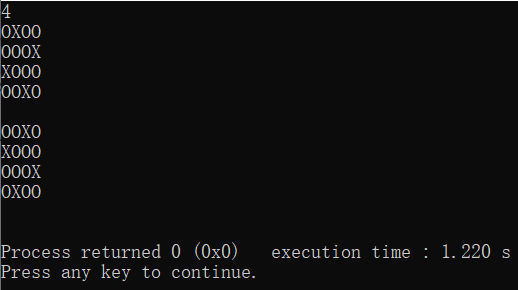
结果

评论(0)